EXPLICACIONES GEOMÉTRICO-DIAGRAMÁTICAS EN FÍSICA DESDE UNA PERSPECTIVA INFERENCIAL

Resumen

El primer objetivo de este artículo es mostrar que explicaciones genuinamente geométricas/matemáticas e intrínsecamente diagramáticas de fenómenos físicos no solo son posibles en la práctica científica, sino que además comportan un potencial epistémico del que sus contrapartes simbólico-verbales carecen. Como ejemplo representativo utilizaré la metodología geométrica de John Wheeler para calcular cantidades físicas en una reacción nuclear. Como segundo objetivo, pretendo analizar la garantía epistémica de este tipo de explicaciones en términos de dependencia sintáctica y semántica entre el contenido de las premisas y la conclusión, lo que denominaremos ‘Criterio de Validez Inferencial’.

Abstract

The main purpose of this paper is to show that geometrical and diagrammatical explanations of physical phenomena are both possible within real-world scientific practices and epistemically advantageous regarding their symbolic-linguistic counterparts. As a way of illustrating these theses, I will analyze John Wheeler’s geometrical procedure for computing relativistic quantities in a nuclear physics scenario. Additionally, I will assess (from an inferential perspective) the epistemic reliability of these particular explanations in terms of an Inferential Validity Criterion, which established a semantic-syntactic dependence relation between explananda and explanandum

¿Sería capaz de explicar un físico teórico el fenómeno de dilatación del tiempo de la teoría de la relatividad especial a un físico experimental sin tener que recurrir a complejas fórmulas usando exclusivamente diagramas? ¿Pueden representaciones o pruebas geométricas dar cuenta rigurosamente de cómo la energía y el momento se conservan en una reacción nuclear? Y en caso de que sea posible, ¿cómo se garantizaría que la información adquirida visualmente mediante diagramas matemáticos nos pueda proporcionar conocimiento empírico? Preguntas de esta índole y sus tentativas respuestas serán el eje del presente artículo.
La cuestión de si las representaciones diagramáticas (figuras geométricas, esquemas formales, animaciones digitales, entre otras) cumplen con un rol decisivo a la hora de explicar hechos intrínseca o genuinamente matemáticos, como pueden ser teoremas o corolarios, se plantea en la actualidad como el tema clave dentro del área disciplinar que se conoce como epistemología del razonamiento visual en matemáticas, especialmente motivado y en ocasiones eclipsado por el intenso debate acerca de las explicaciones matemáticas, tanto en el propio ámbito de la matemática como en el contexto empírico. En este artículo pretenderemos enfrentar los dos debates mencionados de forma simultánea, defendiendo que existen explicaciones geométrico-diagramáticas de fenómenos físicos genuinas. Dicha tesis será justificada desde una perspectiva inferencialista acerca de cómo el contenido empírico válidamente inferido por medio de recursos gráficos y espaciales ofrece una garantía epistémica en la explicación multimodal (Shimojima 2004).
El hecho de que las explicaciones visuales en el ámbito de las ciencias formales y empíricas se presente como una cuestión de pleno interés epistemológico exclusivamente dentro de las dos o tres últimas décadas, y no antes, responde a varios factores vinculados a la evolución intelectual de diferentes disciplinas, a la cual nos acercaremos brevemente en la siguiente sección. En el tercer apartado, nos aproximaremos a la relación entre pruebas y explicaciones diagramáticas en las matemáticas, especialmente en la geometría; en el cuarto, abordaremos la concepción inferencial tanto de la geometría en sí como de su aplicación empírica en el dominio de la física (Bueno y Collyvan 2011). En la quinta sección, expondremos el procedimiento genuinamente geométrico desarrollado por el físico John Wheeler para calcular cantidades de manera diagramática en una reacción nuclear (Wheeler y Taylor 1963). Mediante un criterio de validez inferencial (CVI), desarrollaremos un marco inferencialista para dar cuenta, semántica y sintácticamente, de cómo sería posible ofrecer genuinas explicaciones geométrico-diagramáticas mediante el método de Wheeler de mayor virtuosidad epistémica (simplicidad, potencial descriptivo, accesibilidad, etcétera) que su contraparte verbal.

A mediados del siglo XX, y en pleno giro lingüístico, se consolidó profundamente la vieja idea de que el pensamiento, el conocimiento y la racionalidad humana eran fenómenos intrínsecamente simbólicos en su naturaleza, sobre todo en lo que a nosotros nos concierne en el ámbito de la lógica formal (entendida de modo hegemónico como “lógica simbólica”) o de la matemática abstracta más algebraicista (vívidamente encarnado en el desprecio de los Bourbaki por el uso de imágenes). Ello queda reflejado con claridad en esta sentencia de Ayer
Our knowledge that no observation can ever confute the proposition ‘7 + 5 = 12’ depends simply on the fact that the symbolic expression ‘7 + 5’ is synonymous with ‘12’, just as our knowledge that every oculist is an eye-doctor depends on the fact that the symbol ‘eye-doctor’ is synonymous with ‘oculist’ (1936 113)
Dentro de este amplio contexto intelectual, una prueba matemática (aunque lo mismo se podría decir de una deducción natural lógica) no es otra cosa que una derivación sintáctica de sentencias o cadena de símbolos; por esto un diagrama o una imagen solo podrían desempeñar un papel de mero soporte visual o muleta cognitiva dentro de cualquier práctica en cuanto representaciones epistemológicamente inertes o superfluas, como lo sostiene Tennant (1986). Por supuesto en ello subyace la premisa de que solo las representaciones lingüísticas pueden ser explicativamente relevantes. Sin embargo, el deshielo del simbolocentrismo en ciencias formales llegaría ya al alba del siglo
En primer lugar, debemos entender que a partir de la década de 1990 se produce lo que Mancosu (2005) denomina “renacimiento en visualización”; que no es otra cosa que un cambio de foco de la atención teórica desde las formas de representación simbólicas hacia las visuales. En el ámbito de la lógica formal, Barwise y Etchemendy (1996) abrieron por primera vez la senda de los estudios semánticos sobre los sistemas diagramáticos formales, defendiendo (y demostrando) la importante tesis de que las propiedades metalógicas más fundamentales (completitud, corrección o decidibilidad) son independientes del aparato representacional, sea este simbólico o diagramático.
De hecho, la equivalencia metalógica entre aparatos de representación visual, como el sistema de representación de Grafos Existenciales de Peirce, y la lógica simbólica de predicados ha sido varias veces demostrada, aunque no celebrada, a lo largo del siglo XX (Peirce 1931). Siguiendo la brillante estela peirceana, Sun-Joo Shin (1991) mostró cómo los mecanismos de validez lógica pueden ser implementados a la perfección en sistemas deductivos puramente diagramáticos, entre los cuales cabe mencionar su Venn II (bautizado así por él lógico y diagramático decimonónico)
Si ya en el ámbito lógico el denominado “renacimiento en visualización” rompe enérgicamente con los prejuicios simbolicistas antediluvianos, en la disciplina matemática revolucionó por completo cualquier asunción acerca de cómo hemos de representar visoespacialmente estructuras formales, cómo hemos de derivarlas/probarlas o cómo obtenemos conocimiento a partir de estas. Nótese que la prueba matemática, como explícita derivación sintáctica, constituye el principal mecanismo de esta disciplina para justificar sus teoremas, postulados o principios, y con ello obtener lo que, sin ahondar, denominamos “conocimiento matemático”.
De la era del “diagrams cannot be proof” (Tennant 1986), ya en el ocaso de esta hegemonía iconoclasta en matemáticas, llegamos en un breve periodo de tiempo al rompedor “proofs without words” de Nelsen (1993) o al contundente “proofs and pictures” de Brown (1999), lo cual encarna el paso entre dos formas de comprender la semántica de la representación matemática. Por supuesto, a comienzos del siglo XXI las pruebas matemáticas llevadas a cabo mediante operaciones diagramáticas no solo se considerarán legítimas dentro de gran parte de la comunidad matemática, sino además formalmente rigurosas. En este contexto, Miller (2007) desarrollará un sofisticado sistema formal exclusivamente diagramático para probar teoremas de geometría euclídea
El solo hecho de que las pruebas diagramáticas posean un valor intrínseco en la práctica matemática nos sugiere que la visualizabilidad de contenido matemático pueda ser en cierta forma relevante a la hora de producir conocimiento matemático (aquí entran en juego diversos y variadas cuestiones, como el debate a priori-a posteriori en la adquisición de conocimiento matemático o las implicaciones ontológicas del argumento de indispensabilidad, que por motivos de extensión obviaremos) o la pregunta que es más importante para la primera parte de nuestro argumento en este artículo: ¿es posible ofrecer explicaciones de fenómenos matemáticos por medio de representaciones y operaciones diagramáticas

Antes de proseguir con esta cuestión, debemos tener en cuenta que la minusvaloración epistémica del formato visual que acabamos de señalar brevemente en la sección anterior tiene su inmediato impacto en la reflexión filosófica de su tiempo. El modelo deductivo-nomológico de explicación científica de Nagel, así como sus múltiples variantes, como la versión inductivo-estadística y muchas de sus alternativas cercanas asociarán explicatividad con verbalización y formulación:
The legacy of the DN model, and the focus on linguistic representations in general, in that philosophers have studied scientific explanation without thinking about the contribution of visual representations as if guided by the assumption that only linguistic (or mathematical) representations could be relevant to scientific explanation. Such assumption would be fatal to a study of whether diagrams can play a role in scientific explanation (Perini 2005 258).
A pesar de realizar lo que a mi juicio es un diagnóstico bastante certero, Perini asume implícitamente otra de las tesis que pretenderemos desmontar a lo largo de este artículo: las representaciones matemáticas son siempre representaciones lingüísticas. En sus mismos términos, aceptar esto sería fatal para cualquier estudio acerca de si los diagramas matemáticos cumplen algún rol dentro de la explicación científica. Si las explicaciones genuinamente diagramáticas empiezan a ser un tema candente dentro de la biología (el propio Perini 2005 es un caso de esto), en matemáticas se abordará únicamente de manera colateral a asuntos relacionados con la explicación matemática, y no como un tema de interés propio.
Steiner (1978) recuperó, en términos modernos, la ahora incipiente cuestión de si existen explicaciones matemáticas genuinas. En su planteamiento original, hace referencia al caso específico de aquellas explicaciones matemáticas encargadas de fenómenos puramente matemáticos; o lo que es lo mismo, a aquel tipo de explicación en el que tanto su explanandum como su explanada son de naturaleza intrínsecamente matemática. Su foco se centra en esclarecer, por un lado, cuáles pruebas matemáticas son explicativas y cuáles no, y por otro, señalar por qué razón son explicativas estas últimas; lo interesante es que en el primer ejemplo de pruebas aritméticas acaba involuntaria y colateralmente abarcando el tema de las explicaciones visuales diagramáticas. Tomemos el siguiente teorema:

Teorema 1

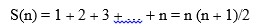
Steiner ofrece una primera prueba por inducción de (1) con carácter exclusivamente simbólico

Teorema 1.1

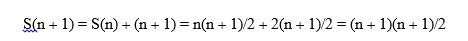
Una segunda prueba simbólica (3) es dada, esta de un carácter más abstracto (se cuantifican secuencias de números y no números individuales) pero más comprensible que la anterior

Teorema 1.2

Por último Steiner admite que la prueba de (1) con mayor capacidad explicativa es aquella que se presenta completamente diagramática y no hace uso de recurso simbólico alguno

Teorema 1.4

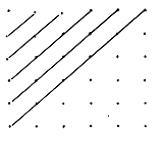
El motivo de que la prueba diagramática (4) sea más explicativa que (3) y sobretodo que (2) es que esta primera permite visualizar el proceso derivativo en el que se prueba la conclusión de (1). Sin embargo, el propio Steiner rechaza la visualizabilidad, como hace también por diferentes motivos con la generalidad y la capacidad de descubrimiento matemático, como criterio explicativo por ser según sus palabras un criterio “demasiado subjetivo”. Nosotros defenderemos más adelante que dicho criterio merecería ser reconsiderado bajo la luz de las últimas evidencias empíricas o al menos analizar por qué la así llamada “visualizabilidad” es explicativamente eficaz con respecto a ciertos teoremas matemáticos. De hecho, en este mismo ejemplo el uso de recursos visuales podría dar cuenta del hecho epistemológico de que la prueba simbólica (3) (cuyos términos aparecen espacialmente desplegados) sea más comprensible que la simbólica-comprimida (2), tal como Steiner apunta.
Dos décadas después del famoso artículo de Steiner, y ya en pleno auge del acercamiento teórico a lo visual desde diferentes ámbitos, Brown (1999) popularizó lo que ahora se conoce técnicamente como “picture-proof”, que no son otra cosa que pruebas matemáticas del estilo de (4) en las que se emplean principalmente recursos visuales para derivar el contenido formal. Nótese que la forma correcta para referirse a este tipo de pruebas, también empleada en la literatura concerniente, es la de “pruebas diagramáticas” (diagrammatic proofs) debido a que las representaciones diagramáticas se caracterizan precisamente por su combinación de elementos visuales con una sintaxis definida, mientras que las representaciones pictóricas no poseen este último ingrediente, clave en la derivación de estructuras formales. Sin embargo, no todas las pruebas diagramáticas poseen ni mucho menos un claro y definido carácter explicativo.
Pero, ¿en qué sentido una prueba formal puede ser explicativa? Varias han sido las respuestas a esta pregunta, y las más destacadas serían: 1) en la capacidad de realzar elementos característicos del fenómeno a derivar (modelo de explicación local de Steiner) y 2) en remarcar visualmente elementos estructurales clave en la derivación (Brown 1999). Más allá de estas respuestas iniciales, Giaquinto establece un criterio teórico algo más sofisticado para saber cuándo una prueba formal explica:
Criterio de Explicación en Pruebas Formales (CEPF): una prueba formal es explicativa si y solo si cualquier agente cognitivo que comprende la prueba podría llegar a saber el motivo de por qué el contenido de la conclusión se deriva sintácticamente de la prueba.
Es decir, lo que Giaquinto propone con su criterio sería reconocer que una explicación de este tipo no es otra cosa que la capacidad de obtener conocimiento válido sobre cómo el contenido formal de la conclusión se basa en la comprensión de dicha derivación. Es decir, (4) es explicativo con respecto a (1) debido a que los motivos que me llevan a comprender cómo se derivan diagramáticamente las líneas diagonales me llevan también a saber cómo funciona la progresión aritmética (1). Seguiremos profundizando en esta idea. Para aplicar este o cualquier otro criterio de explicación (o mejor de capacidad explicativa o “explicatividad”), tomemos como caso estas tres pruebas del sempiterno teorema de Pitágoras:

Figura 1. Tres pruebas visuales del teorema de Pitágoras

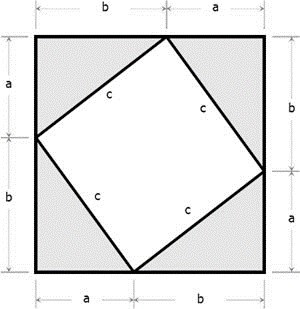
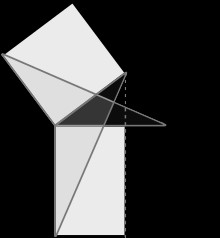
La primera (5) es la famosa prueba del teorema de Pitágoras que encontramos en el I.47 de los Elementos de Euclides, que representa sincrónicamente cada uno de los pasos requeridos. A pesar de comportar una pulcrísima derivación formal del teorema en cuestión (claro ejemplo de lo que podríamos calificar inferencialmente como “deducción diagramática”) sería difícil justificar que tal derivación gráfica explica de alguna forma el teorema: comprender cómo se lleva a cabo dicha derivación no genera ningún conocimiento relevante con respecto al teorema.
En cuanto a las virtudes epistémicas de la prueba diagramática (6), podríamos hablar al menos de potencial intuitivo o “facilitación comprensiva” sobre cómo se deriva el teorema ENT#091;de la misma forma que (3) facilitaba más la comprensión de (1) que (2)ENT#093;. Sin embargo, ¿podríamos hablar de prueba explicativa según Giaquinto? A pesar de facilitar la comprensión geométrica del teorema de Pitágoras, la construcción de (6) no nos aporta información significativa acerca de por qué es posible derivar el teorema.
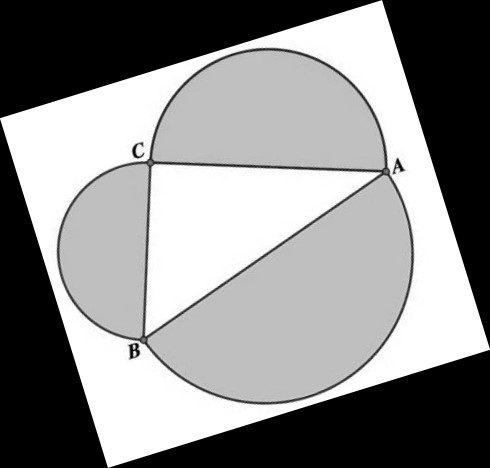
Por último, pero no por ello la menos importante, la prueba (7) puede llegar a presentarse a primera vista como contraintuitiva. Sin embargo, una vez el agente cognitivo ha comprendido cómo se deriva la prueba (es decir, que el área combinada de los lados menores coincide con el área adjunta al lado mayor), esto propicia en él un conocimiento justificado sobre esta derivación no rígida del teorema. Como apoyo intuitivo bastaría con recrear materialmente o por medio de imágenes mentales las dos áreas grisáceas menores como recipientes repletos de líquido y el área mayor como un recipiente vacío, de manera que al verter el líquido de los dos primeros sobre el último, este se llenaría exactamente en su capacidad.

Hemos de reconocer que el CEPF de Giaquinto da cuenta satisfactoriamente de por qué una prueba formal puede llegar a ser explicativa en términos de la dinámica de estados cognitivos en el agente epistémico; sin embargo, ni determina ni aclara cuáles son los mecanismos inferenciales subyacentes a este fenómeno. En este último sentido, no sería deseable incorporar el componente inferencial (es decir, cómo la información contenida al inicio del proceso se deriva por medio de operaciones discretas y algorítmicamente delimitadas hasta obtener un estado final) al cognitivo en nuestra propuesta naturalista, buscando clarificar de qué manera es epistemológicamente ventajoso en ciertas prácticas científicas usar inferencialmente representaciones visuales en vez de simbólicas.
Entre los autores que siguen esta línea metodológica a la que nos adscribimos encontramos a Norman (2004), quien nos sugiere que los diagramas constituyen soportes inferenciales sintácticamente sólidos que justifican ciertas creencias visualmente generadas en la práctica matemática (como construcción de pruebas y derivación de corolarios). No podemos obviar la interesante interpretación inferencialista por parte de Mumma (2010) de los procedimientos diagramáticos que uno puede encontrar desde hace veintitrés siglos en los Elementos de Euclides. Mientras Miller, como ya hemos mencionado, construye un aparato deductivo formal a partir de los diagramas euclídeos, Mumma asume que las inferencias informales (aquellas que operan sobre piezas de información parcial, por ejemplo, la abducción de información geométrica mediante la postulación de líneas secantes) también cumplen un rol epistemológico importante en la misma obra.
En este punto cabe preguntarse cuál es el particular comportamiento inferencial de las representaciones y operaciones diagramáticas. Según Atsushi Shimojima (1996), discípulo intelectual de Barwise y Etchemendy, dedicado a la investigación tanto teórica como empírica de la condición inferencial de los diagramas, las transformaciones diagramáticas (genéricas, de cualquier índole) se basan en el uso de propiedades espaciales del medio representacional de donde adquieren su potencial inferencial frente a las representaciones simbólicas. El uso de recursos espaciales, carácter fundamental y constitutivo de las inferencias diagramáticas, tal y como señala Shimojima, no se restringe a las propiedades geométricas del espacio (por ejemplo, nótese que el poder explicativo de (4) depende de que exista la misma distancia entre todos los puntos de la red) sino que también las propiedades espaciales más abstractas o topológicas cumplen con un rol sintáctico-semántico, cuyo caso paradigmático se encuentra en los diagramas de Venn o su reformulación en Shin (1991), en donde las relaciones topológicas entre áreas tienen un significado algebraico-booleano definido: intersección por conjunción, unión por disyunción, etc.
Dicha distinción entre el uso de recursos geométricos y topológicos se recuperará ortogonalmente con la propuesta de Manders (2008) de distinguir entre propiedades exactas (o “métricas”), como puede ser la relación de congruencia entre dos figuras (nótese como la prueba (6) depende de la congruencia de los cuatro triángulos rectángulos) y propiedades co-exactas (o “topológicas”), como es el caso de intersecciones entre elementos o el hecho de que el área de las regiones sombreadas en (7) sea independiente de su forma.
Hasta ahora solo nos hemos dedicado a explorar el carácter inferencial de las explicaciones diagramático-matemáticas de fenómenos matemáticos (MEM), sin embargo, sería interesante plantearnos la pregunta acerca de si el rango disciplinar de dichas formas explicativas solo se restringe al ámbito de las ciencias formales o, por el contrario, también se encontraría aplicación en las ciencias empíricas. ¿Existen las MEP o explicaciones matemáticas de fenómenos físicos? Pocos temas han despertado mayor controversia que este en los últimos años dentro de la filosofía de la ciencia en general y de la epistemología de la matemática aplicada en particular. Sin embargo, la cuestión específica que nos concierne en este artículo no sería sino dilucidar si existen explicaciones intrínsecamente diagramático-matemáticas de fenómenos físicos, lo cual, por supuesto, complica aún más el escenario del que debemos hacernos cargo.
Curiosamente, nuestro acento en el carácter inferencial de las explicaciones no solo nos brinda luz sobre cómo la información contenida en el explanandum es derivada desde el explananda, sino que también puede dar cuenta de la relación aplicativa entre matemáticas y el ámbito empírico. Entre las varias y diversas posiciones teóricas desarrolladas en torno al debate sobre si las MEP existen y de qué manera lo hacen, nos encontramos la conocida como concepción inferencialista de la aplicabilidad de las matemáticas promovida por Ottavio Bueno y Mark Colyvan (2011). En ella se defiende la idea de que las estructuras matemáticas pueden llegar a contener información empírica por medio de relaciones interestructurales, tales como homeomorfismos o isomorfismos entre el ámbito formal y el ámbito físico. Uno de los puntos más interesantes de esta propuesta es que aquellos mecanismos inferenciales llevados a cabo sobre estructuras matemáticas se transfieren (vía homeo/isomorfismo) al medio empírico, o lo que es lo mismo, la derivación sintáctica que comportan las inferencias matemáticas ha de interpretarse como manipulación operacional sobre cierto contenido físico.
En una línea argumental similar encontramos la propuesta de Molinini (2016) en relación con el valor epistemológico de los aquí omnipresentes diagramas euclídeos. Este autor propone que se recurre al potencial inferencial de las representaciones geométrico-diagramáticas con contenido físico en lo que él denomina “inferencias inherentes”, en donde se posibilita que las propiedades matemáticas codifiquen información de carácter físico. Tomemos como ejemplo el proceso de inferir cuál será la dirección que seguirá un cuerpo con velocidad constante tras colisionar elásticamente con un segundo cuerpo. Mediante la suma de dos vectores podremos obtener diagramáticamente un tercer vector, correspondiente a la diagonal del paralelogramo construido a partir de los dos vectores iniciales (véase figura 2); la inferencia inherente de esta operación diagramática nos muestra cómo a través de emplear recursos geométricos podemos obtener información física sobre cuál será la dirección que tomará el primer cuerpo tras la colisión:

Figura 2. Inferencia inherente de la dirección de un cuerpo tras una colisión

El físico teórico John Wheeler desarrolló en uno de los capítulos de su libro Spacetime Physics (Wheeler y Taylor 1963) un método intrínsecamente visual-diagramático, el cual no requería de codificar información empírica mediante fórmulas simbólicas para calcular con precisión valores cuantitativos dentro del ámbito experimental de colisiones de alta energía en física relativista de partículas. Como ejemplo ilustrativo, Wheeler toma una reacción nuclear en la que un deuterón (isótopo del hidrógeno compuesto por un protón y un neutrón) acelerado, y en consecuencia altamente energético, colisiona contra un deuterón en reposo, produciendo en consecuencia un protón y un tritio (otro isótopo del hidrógeno, este compuesto por un protón y dos neutrones). Tras la colisión se generan los valores de energía y momento de los dos deuterones reactantes, con lo que por medio de las leyes de conservación se obtiene relativistamente la masa de ambos y del protón resultante. Sin embargo, para calcular o inferir la masa del tritio resultante se requeriría una computación algo más compleja de los valores disponibles. Por supuesto, y como es habitual, dicha computación se llevó a cabo por medio de manipulación algebraica de fórmulas simbólicas. La novedad metodológica de Wheeler recae en llevar a cabo esa misma computación por medio de operaciones diagramáticas con elementos geométricos.
En primer lugar, se construye un sistema tetradimensional de coordenadas, desde donde se representan las cantidades tanto de energía (eje vertical) o, lo que es relativistamente equivalente, masa en reposo, como de las tres dimensiones del momento (eje horizontal y de profundidad). Con el objetivo de evitar representar contenido físico redundante y de economizar los recursos visuales empleados en el sistema diagramático, una de las dimensiones del momento (Pz) será suprimida; por lo que partiríamos de un sistema diagramático tridimensional proyectado en las dos dimensiones del formato del libro original o el presente artículo.
En segundo lugar, la masa-energía o (por acortar) masa de cada una de las cuatro partículas que intervienen en la colisión, codificada en la física relativista por 4-vectores, queda representada mediante segmentos. Como punto de partida (valores iniciales) contamos con tres segmentos: AB se presenta como la masa del deuterón “bombardero”, 0A como la masa del deuterón en reposo (que su segmento-masa coincida con el eje de energía/masa en reposo “E” significa o representa el hecho físico de que este segundo deuterón no contiene energía cinética) y 0B como la masa total de la reacción. Además de los segmentos mencionados, tenemos también los ángulos abiertos entre los segmentos, los cuales codifican información sobre las “velocidades relativas” existentes entre las partículas en cuestión (por ejemplo, el ángulo 0AB representa la velocidad relativa entre los dos deuterones). En este mismo sentido, el triángulo 0AB representa de modo visual y diagramático las cantidades físicas del escenario previo a la reacción. A partir de estos elementos geométricos se ha de derivar el segmento correspondiente a la masa del tritio. ¿Cómo se llevaría esto a cabo?
One determines the triton mass value by using the conservation laws much as a surveyor finds the length of one side of a polygon from the other measurements of the polygon by using Euclidean geometry (Wheeler y Taylor 1963 225).
La clave, tal y como el propio Wheeler confiesa en la cita anterior, está en la geometría euclídea, donde encontraremos las reglas diagramáticas necesarias para obtener el dato final requerido. A partir de los segmentos CP y CE (que representan los componentes “y-momento” y “energía”, respectivamente, del 4-vector masa del protón resultante) y por medio del teorema de Pitágoras, es posible obtener el segmento C0 que codifica la masa-energía del protón. Es entonces cuando uniendo CB se puede derivar el buscado segmento CB (coloreado en rojo en la figura 3), el cual encapsula por medio de su longitud el valor correspondiente a la masa-energía del tritio.

Figura 3. Inferencia diagramática de la masa del tritio en la reacción nuclear por medio de la metodología geométrica de Wheeler y Taylor (1963)

Es, cuanto menos, semánticamente interesante, que en el contexto semántico de este sistema diagramático la geometría euclídea representa la geometría física lorentziana propia del espacio- tiempo especial relativista. Desde una perspectiva inferencial como aquí hemos defendido, realizar inferencias diagramáticas por medio de la geometría euclídea en este contexto supone (o “inhiere”, en términos de Molinini 2016) manipular información física sobre la estructura geométrica del espacio-tiempo. Esto es fundamental, no solo en la dimensión sintáctico-formal sino también en el plano semántico, de forma que toda operación diagramática correcta (es decir, que sea desarrollada según la geometría euclídea) implica la preservación del contenido físico de sus elementos geométricos: por ejemplo, al derivar el segmento CB, el contenido de AB, la masa del deuterón incidente, no se ve modificado.

Una vez ha sido esbozada la metodología visogeométrica wheeleriana como caso paradigmático, podemos apuntar que lo verdaderamente importante que subyace a cualquier explicación, tal y como defendemos en este artículo, se formularía como pregunta de la siguiente manera: ¿constituye la derivación diagramática del segmento CB a partir de los elementos geométricos iniciales un proceso inferencial válido? Si con “inferencialmente válido” nos referimos a “lógica o deductivamente válido”, entonces la respuesta es No; pues tal y como dice Molinini “not all thinking is a matter of making inferences in the same way that logic-based systems do” (2016 418). Por otro lado, si nos referimos más bien a un tipo de inferencia informal sobre fragmentos de información parcial, como es común en la enorme mayoría de la práctica científica, entonces sería necesario formular:
Criterio de Validez Inferencial (CVI): una inferencia es válida si como consecuencia de realizar correctamente todas operaciones necesarias para derivar sintácticamente la conclusión, entonces la información contenida en la conclusión deriva semánticamente de la información contenida en las premisas. O, dicho de otra forma, una inferencia es válida si el contenido informacional de la conclusión depende tanto sintáctica como semánticamente del contenido informacional de las premisas.
No es posible dar cuenta de ninguna inferencia explicativa si no tenemos antes una mínima, pero suficiente garantía de que lo inferido sea consecuencia, no lógica pero sí semántica y sintáctica, de las premisas. Solo a partir de esta mínima garantía podemos hablar de explicación o cualquier otro fenómeno epistemológico con una arquitectura de inferencia.
En este punto, y con base en lo argumentado expondré directamente mi tesis con respecto al procedimiento wheeleriano: es posible explicar un fenómeno físico tan significativo como la conservación de la energía-momento relativista en una reacción nuclear por medio exclusiva y genuinamente de representaciones diagramáticas y operaciones geométricas. Con ello estoy afirmando simultáneamente: 1) que las explicaciones genuinamente matemáticas de fenómenos físicos se dan en la práctica científica, y 2) que las explicaciones diagramáticas son herramientas epistemológicas clave en muchos ámbitos y disciplinas. Otras alternativas previas a la nuestra, por ejemplo el CEPF de Giaquinto (analizado en la sección 2) parecen no dar cuenta, más allá de lo que ocurre a nivel psicológico, de las condiciones de posibilidad de tal explicación o prueba geométrica explicativa.
Aplicación de Modelo Cognitivo de CEPF (Giaquinto 2015): comprender por qué el segmento 0B sea una arista tanto para el triángulo 0AB como para el triángulo 0CB (lo cual es un hecho incontrovertida y genuinamente geométrico) posibilita en el agente cognitivo una explicación sobre por qué la cantidad de masa-energía antes de la colisión es equivalente a la cantidad de masa-energía después de la colisión.
Más allá de ofrecer una historia cognitiva de cómo ocurre una explicación diagramática (la comprensión del contenido visual de una representación mental del explanandum geométrico genera los recursos cognitivos requeridos para explicar el explananda físico) sería deseable contar con un modelo que analizase cuáles son las condiciones inferenciales que garantizan el valor explicativo de un soporte genuinamente diagramático-geométrico con respecto a un fenómeno físico. Con base en el CVI como condición explicativa, nuestra propuesta es la siguiente:

Figura 4. Explicación geométrica-diagramática (Wheeler y Taylor 1963) de la validez de la ley relativista de conservación de la masa, representada mediante fórmulas en una reacción nuclear

Aplicación del Modelo Inferencial de Explicación (MEP): abducir válida y visualmente por medio de representaciones diagramáticas que el segmento 0B (coloreado de rojo en la figura 4) sea una arista tanto para el triángulo 0AB como para el triángulo 0CB signifique que la cantidad de masa-energía antes de la colisión es equivalente a la cantidad de masa-energía después de la colisión posibilita explicar este fenómeno físico (independientemente de cómo esté representado) a partir de los recursos espaciales-geométricos que codifican diagramáticamente las leyes relativistas de conservación de la masa-energía.
El que un aparato diagramático (que forma parte representacional de una prueba o no) resalte la visualización y uso de recursos espaciales a la hora de representar su contenido formal o empírico, y sin que por ello disminuya su expresividad o rigor sintáctico, es una condición necesaria pero no suficiente, tal y como defendía Steiner (1978), para su explicatividad. Por ello la prueba (6) del teorema de Pitágoras, a pesar de expresar intuitivamente su contenido y gozar de la virtud epistémica de la visualización, no posee la condición que nosotros consideramos constituyente de toda explicación: la validez inferencial (CVI). Esta fuerte condición semántico-semántica hace posible que una representación diagramática puede explicar genuinamente y con garantías epistémicas un fenómeno físico.
Al igual que en la práctica matemática, los diagramas en física cumplen con diferentes funciones según sus características estructurales y representacionales, y por supuesto no todos ellas son explicativas. En el caso de los famosos diagramas de Feynman, su valor científico (en contra de la creencia popular) reside en su capacidad de simplificar computacionalmente conjuntos de integrales multivariables complejas y no en explicar cómo sucede en diversas interacciones fundamentales, precisamente porque tales mecanismos de interacción no quedan diagramáticamente codificados en las propiedades visoespaciales del mismo. Abducir visualmente que un diagrama de Feynman representa una interacción fundamental constituye una inferencia inválida, y por tanto cualquier explicación basada constitutivamente en tal inferencia sería cuanto menos epistémicamente inerte. Por otro lado, tenemos que existen diagramas con gran capacidad de codificar visualmente el contenido físico de determinadas teorías, como es el caso de los diagramas de Minkwoski, cuyo potencial explicativo, si alguno, depende de aprovechar su alta complejidad representacional (por ejemplo, la superficie de los conos de luz no representan ninguna estructura espacio-temporal sino un límite máximo en la aceleración).

Figura 5. Representaciones diagramáticas empleadas en física: diagrama de Feynman (izquierda), diagrama de Minkowski (centro) y diagrama de Wheeler (derecha)

De este modo, las posibilidades epistémicas de cada tipo de diagrama en las ciencias físicas, al igual que en matemáticas, tal y como vimos la tercera sección, dependen no exclusivamente del agente cognitivo (en oposición a Giaquinto 2015) sino sobre todo de cómo se emplean representacionalmente los recursos visoespaciales para codificar información sobre el fenómeno empírico en cuestión

Para concluir cabría recalcar una vez más, sin riesgo a ser repetitivo, una de las tesis principales que hemos venido defendiendo hasta aquí: el potencial epistémico, en general, y la capacidad explicativa, en particular, de un diagrama geométrico-topológico viene determinada por la forma en la que se usan los recursos visoespaciales para codificar información genuinamente matemática o intrínsecamente empírica, según el explananda sea un fenómeno matemático o físico, respectivamente. Desde el marco inferencial desplegado y a partir del CVI, hemos analizado cómo el componente de garantía epistémica que comporta nuestro ejemplo de explicación diagramático-geométrica de la conservación de energía y momento bajo la metodología wheeleriana puede ser satisfactoriamente evaluado en términos de independencia representacional (simbólica, verbal, diagramática…) del contenido informacional y dependencia sintáctica y semántica del contenido informacional diagramáticamente derivable del contenido informacional de las premisas o datos iniciales, independientemente del formato en las que estos se presenten.
También hemos de mencionar (como tema colateral) el hecho de que una de las características epistémicas más interesantes de este tipo de diagramas es la de poseer, en términos generales, un nivel de inteligibilidad mayor que sus versiones simbólicas, debido precisamente al uso de mecanismos gráficos que incentivan la comprensibilidad directa del fenómeno físico. De esta forma, y con este ilustrativo caso, hemos mostrado cómo las explicaciones diagramático-geométricas de fenómenos físicos no solo son posibles (respondiendo simultáneamente tanto al debate sobre las explicaciones visodiagramáticas como al debate sobre las explicaciones matemáticas) sino que además en muchos casos son epistémicamente superiores a sus contrapartes verbales. Aún queda mucha labor que realizar, tanto en lo filosófico como en lo empírico, para entender la vital importancia de las representaciones diagramáticas a la hora de generar y gestionar conocimiento en las prácticas científicas del día a día.

• Ayer, A. J., 1936. Language, Truth and Logic. London: V. Gollancz.
• Brown, J., 1999, Philosophy of Mathematics: an introduction to the world of proofs and pictures, London: Routledge.
• Barwise, J. and J. Etchemendy, 1996, “Visual information and valid reasoning”, in Logical Reasoning with Diagrams, G. Allwein and J.
• Barwise (eds) Oxford: Oxford University Press.
• Bueno, O. and M. Colyvan, 2011, “An Inferential Conception of the Application of Mathematics”, Noûs, 45: 345–374.
• Bueno, O. and S. French, 2012, “Can Mathematics Explain Physical Phenomena?”, British Journal for the Philosophy of Science, 63 (1): 85–113.
• Giaquinto, M., 1994, “Epistemology of visual thinking in elementary real analysis”, British Journal for the Philosophy of Science, 45: 789–813.
• –––, 2007, Visual Thinking in Mathematics, Oxford: Oxford University Press.
• Hafner, J. and P. Mancosu, 2005, “The Varieties of Mathematical Explanation”, in P. Mancosu et al. (eds.), Visualization, Explanation and Reasoning Styles in Mathematics, Berlin: Springer, 215–250.
• Jones, N., 2014, “Bowtie Structures, Pathway Diagrams and Topological Explanation”, Synthese, 79: 1135–1155.
• Lange, M., 2016, “Explanatory Proofs and Beautiful Proofs”, Journal of Humanistic Mathematics, 6 (1): 8–51.
• Lyon, A., 2012, “Mathematical Explanations of Empirical Facts, and Mathematical Realism”, Australasian Journal of Philosophy, 90 (3): 559–578.
• Mancosu, P., 2005, “Visualization in Logic and Mathematics”, in P. Mancosu, K. Jørgensen and S. Pedersen (eds), Visualization, Explanation and Reasoning Styles in Mathematics, Dordrecht: Springer.
• Manders, K., 2008, The Euclidean Diagram. In Paolo Mancosu (ed.), The Philosophy of Mathematical Practice. Oxford University Press. pp. 80--133.
• Miller, N., 2007, Euclid and His Twentieth Century Rivals: Diagrams in the Logic of Euclidean Geometry. Center for the Study of Language and Inf.
• Molinini, D., 2016. The Epistemological Import of Euclidean Diagrams. Kairos. Journal of Philosophy and Science 16 (1):124-141.
• Needham, T., 1997, Visual Complex Analysis, Oxford: Clarendon Press.
• Norman, J., 2004. Can diagrams have epistemic value? The case of Euclid. In A. Blackwell, K. Marriott & A. Shimojima (eds.), Diagrammatic Representation and Inference. Springer. pp. 14--17.
• Peirce, C.S. 1931,. Collected Papers of Charles Sanders Peirce. Cambridge: Harvard University Press.
• Perini, L., 2005. Explanation in two dimensions: Diagrams and biological explanation. Biology and Philosophy 20 (2-3):257-269.
• Saatsi, J., 2018, “On Explanations from Geometry of Motion”, The British Journal for the Philosophy of Science, 69 (1): 253–273.
• Shin, S., 2004, Heterogeneous reasoning and its logic. Bulletin of Symbolic Logic 10 (1):86-106.
• –––, 1991. Valid Reasoning and Visual Representation. Dissertation, Stanford University
• Shimojima, A, 1996,. Operational constraints in diagrammatic reasoning. In Gerard Allwein & Jon Barwise (eds.), Logical Reasoning with Diagrams. Oxford University Press.
• –––,2004. Inferential and expressive capacities of graphical representations: Survey and some generalizations. In A. Blackwell, K. Marriott & A. Shimojima (eds.), Diagrammatic Representation and Inference. Springer. pp. 18--21.
• Steiner, M., 1978a, “Mathematical Explanation”, Philosophical Studies, 34: 135–151.
• Tennant, N. 1986,. The Withering Away of Formal Semantics? Mind and Language 1 (4):302-318.
• Wheeler, J. A., y Taylor, E. F., 1963, Spacetime Physics, A Series of Books in Physics. W. H. Freeman and Company.